Matlab adalah singkatan dari MATrix LABoratory, merupakan bahasa pemrograman yang dikembangkan oleh The Mathwork Inc. yang hadir dengan fungsi dan karakteristik yang berbeda dengan bahasa pemrograman lain yang sudah ada lebih dahulu seperti Delphi, Basic maupun C++. Matlab merupakan bahasa pemrograman level tinggi yang dikhususkan untuk kebutuhan komputasi teknis, visualisasi dan pemrograman seperti komputasi matematik, analisis data, pengembangan algoritma, simulasi dan pemodelan dan grafik-grafik perhitungan Pada awalnya Matlab dibuat untuk memberikan kemudahan mengakses data matrik pada proyek LINPACK dan EISPACK. Saat ini matlab memiliki ratusan fungsi yang dapat digunakan sebagai problem solver mulai dari simple sampai masalah-masalah yang kompleks dari berbagai disiplin ilmu.
Dalam lingkungan perguruan tinggi teknik, Matlab merupakan perangkat standar untuk memperkenalkan dan mengembangkan penyajian materi matematika, rekayasa dan kelimuan. Di industri, MATLAB merupakan perangkat pilihan untuk penelitian dengan produktifitas yang tinggi, pengembangan dan analisanya.
Kegunaan MatLab secara umum adalah sebagai berikut:
a) Matematika dan komputasi,
b) Perkembangan algoritma,
c) Pemodelan, simulasi, dan pembuatan prototype,
d) Analisa data, eksplorasi dan visualisasim
e) Pembuatan aplikasi, termasuk pembuatan antaramuka grafis.
Karakteristik MATLAB :
- Bahasa pemrogramannya didasarkan pada matriks (baris dan kolom).
- Lambat (dibandingkan dengan Fortran atau C) karena bahasanya langsung diartikan.
- Automatic memory management, misalnya kita tidak harus mendeklarasikan arrays terlebih dahulu.
- Tersusun rapi.
- Waktu pengembangannya lebih cepat dibandingkan dengan Fortran atau C.
- Dapat diubah ke bahasa C lewat MATLAB Compiler.
- Tersedia banyak toolbox untuk aplikasi-aplikasi khusus.
Beberapa kelebihan Matlab jika dibandingkan dengan program lain seperti Fortran, dan Basic adalah :
- Mudah dalam memanipulasi struktur matriks dan perhitungan berbagai operasi matriks yang meliputi penjumlahan, pengurangan, perkalian, invers dan fungsi matriks lainnya.
- Menyediakan fasilitas untuk memplot struktur gambar (kekuatan fasilitas grafik tiga dimensi yang sangat memadai).
- Script program yang dapat diubah sesuai dengan keinginan user.
- Jumlah routine-routine powerful yang berlimpah yang terus berkembang.
- Kemampuan interface (misal dengan bahasa C, word dan mathematica).
- Dilengkapi dengan toolbox, simulink, stateflow dan sebagainya, serta mulai melimpahnya source code di internet yang dibuat dalam matlab( contoh toolbox misalnya : signal processing, control system, neural networks dan sebagainya).
Lingkungan Kerja MATLAB :
Secara umum lingkungan kerja Matlab terdiri dari tiga bagian yang penting yaitu:
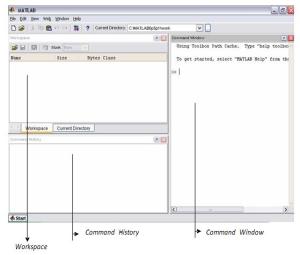
1. Command Windows
Windows ini muncul pertama kali ketika kita menjalankan program Matlab. Command windows digunakan untuk menjalankan perintah-perintah Matlab, memanggil tool Matlab seperti editor, fasilitas help, model simulink, dan lain-lain. Ciri dari windows ini adalah adanya prompt (tanda lebih besar) yang menyatakan Matlab siap menerima perintah. Perintah tersebut dapat berupa fungsi-fungsi bawaan (toolbox) Matlab itu sendiri.
- Workspace: Menampilkan semua variable yang pernah dibuat meliputi nama variable, ukuran, jumlah byte dan class.
- Command History : Menampilkan perintah-perintah yang telah diketikkan pada command Window.
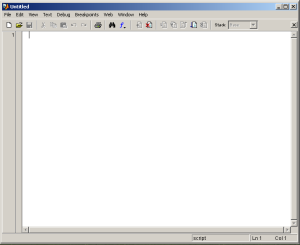
2. Editor Windows
Windows ini merupakan tool yang disediakan oleh Matlab yang berfungsi sebagai editor script Matlab (listing perintah-perintah yang harus dilakukan oleh Matlab). Ada dua cara untuk membuka editor ini, yaitu:
- Klik : File, lalu New dan kemudian M-File
- Ketik pada command windows : ”edit”
Secara formal suatu script merupakan suatu file eksternal yang berisi tulisan perintah MatLAb. Tetapi script tersebut bukan merupakan suatu fungsi. Ketika anda menjalankan suatu script, perintah di dalamnya dieksekusi seperti ketika dimasukkan langsung pada MatLAb melalui keyboard.
M-file selain dipakai sebagai penamaan file juga bisa dipakai untuk menamakan fungsi, sehingga fungsi fungsi yang kita buat di jendela editor bisa di simpan dengan ektensi .m sama dengan file yang kita panggi dijendela editor. Saat kita menggunakan fungsi Matlab seperti inv, abs, cos, sin dan sqrt, matlab menerima variabel berdasarkan variabel yang kita berikan. Fungsi M-file mirip dengan script file dimana keduanya merupakan file teks dengan ektensi .m . sebagaimana script M-file, fungsi m-file tidak dimasukkan dalam jendela command window tetapi file tersendiri yang dibuat dengan editor teks.
Membentuk dan menjalankan M-File:
- Klik menu File, pilih New dan klik M-File
- Pada editor teks, tulis argumen atau perintah
- Simpan dengan cara klik File, pilih Save As dan beri nama dengan ekstensi .m
- Pastikan file yang akan dijalankan berada pada direktori aktif
- Misalkan file graf1.m berada di C:\MATLAB, maka lakukan perintah cd
- >> cd c:\matlab
- Kemudian jalankan file graf1.m dengan cara
- >> graf1
3. Figure Windows
Windows ini merupakan hasil visualisasi dari script Matlab. Matlab memberikan kemudahan bagi programmer untuk mengedit windows ini sekaligus memberikan program khusus untuk itu, sehingga selain berfungsi sebagai visualisasi output yang berupa grafik juga sekaligus menjadi media input yang interaktif.
- Simulink windows.
Windows ini umumnya digunakan untuk mensimulasikan system kendali berdasarkan blok diagram yang telah diketahui. Untuk mengoperasikannya ketik “simulink” pada command windows.
Karakter Spesial MatLab
- Tanda % merupakan penanda komentar. Keterangan setelah tanda tersebut akan diabaikan dalam proses perhitungan. Contoh :
y = 2:2:8 % y = [2468];
y = 2.00 4.00 6.00 8.00
- Tanda ; merupakan perintah pembatas yang tidak ditampilkan di jendela kerja, merupakan pemisah kolom dan baris dalam matriks. Contoh :
A = [1 3 5 ; 5 3 1];
- Tanda : merupakan pembatas jangkauan, contohnya :
B = [0:2:8]
B = 0.00 2.00 4.00 6.00 8.00
- Tanda ` merupakan transpose matriks yang merupakan suatu vector kolom
X = [3 2 4 5;7 6 5 8]
X= 3.00 2.00 4.00 5.00
7.00 6.00 5.00 8.00
X=X `
X= 3.00 7.00
2.00 6.00
4.00 5.00
5.00 8.00
- Tanda … digunakan untuk menuliskan baris perintah yang panjang contohnya:
P = sin(1) – sin(2) + sin(3) – sin(4) + sin(5) + cos(6) + … cos(7) – cos(8) + cos(9) – cos(10) + cos(11) + cos(12)
P = 1.0273
Contoh dan fungsi kode yang dapat diketik pada command windows :
>> help ¿ : Menunjukkan semua help topic di Matlab.
>>what general ¿ : Menunjukkan instruksi-instruksi yang tersedia di
direktori general, salah satunya adalah instruksi clear.
>>help general ¿ : Menunjukkan instruksi-instruksi yang tersedia di
direktori general , dan fungsinya secara umum.
>>help clear ¿ : Menunjukkan penjelasan detail untuk instruksi clear.
(Fungsinya untuk apa, syntaxnya untuk apa, fungsi lain yang terkait apa)
>> help ops ¿ : Menunjukkan penulisan operator2 di dalam Matlab.
>>clc; ¿
>>x ¿
clc digunakan untuk membersihkan layar, tetapi nilai variable yang tersimpan dimemori tidak akan hilang sehingga dapat ditampilkan kembali ke layer dengan memanggil nama variabelnya.
>>clear; ¿
>>x ¿
clear digunakan untuk membersihkan layer sekaligus menghapus variable dari memori sehingga kita tidak dapat menampilkan nilai variable ke layer. (muncul pesan ??? Undefined function or variable ‘x’.)
>> x=4;
>> y=5;
>> z=x+y;
>> z
Merupakan contoh barisan instruksi untuk melakukan penjumlahan.
Angka dan Operasi Aritmatika
Ada tiga jenis angka di MATLAB yaitu :
- Bilangan bulat yaitu bilangan yang tidak mengandung desimal. Contohnya: >> xi = 10
- Bilangan real yaitu bilangan yang mengandung desimal contohnya :>> xr = 12.6054 >> realmax % batas atas bilangan real di matlab
ans = 1.7977e+308
>> realmin % batas minimum bilangan real di matlab
ans = 2.2251e-308 - Bilangan kompleks
>> i
ans = 0 + 1.0000i
>> x = 1 + sqrt(3)*i
x = 1.0000 + 1.7321i
>> A= [1 j;-j*5 2]
A= 1.0000 0 + 1.0000i
0 – 5.0000i 2.0000
Beberapa penggunaan operator aritmatika antara dua operand (A dan B) ditunjukkan pada tabel berikut ini :
| Operasi | Simbol |
| Penambahan | + |
| Pengurangan | – |
| Perkalian | * |
| Pembagian | / atau \ |
| perpangkatan | ^ |
Variabel Pada Matlab
Matlab memiliki tiga variabel sebagai nonnumbers yaitu:
- –Inf (Negative Infinity)
- Inf (Infinity)
- Nan (Not an number)
Matlab hanya memiliki dua jenis tipe data yaitu Numeric dan String. Dalam matlab setiap variabel akan disimpan dalam bentuk matrik. User dapat langsung menuliskan variabel baru tanpa harus mendeklarasikannya terlebih dahulu pada command window. Contoh pembuatan variabel pada matlab:
Penamaan variabel pada matlab bersifat caseSensitif karena itu perlu diperhatikan penggunaan huruf besar dan kecil pada penamaan variabel. Apabila terdapat variabel lama dengan nama yang sama maka matlab secara otomatis akan me-replace variabel lama tersebut dengan variabel baru yang dibuat user.
Fungsi Pemrograman Dalam MATLAB
Fungsi Dasar
1. Fungsi Matematika Dasar
Tabel 1.1a Fungsi Matematika Dasar
| Fungsi | Keterangan |
| Abs | Menghitung nilai absolut |
| Exp | Memperoleh nilai dari e pangkat bilangan tertentu (e = 2.718282) |
| log | Menghitung logaritma natural (ln) suatu bilangan |
| Sqrt | Menghitung akar pangkat 2 dari suatu bilangan |
| Ceil | Membulatkan bilangan ke bilangan bulat terdekat menuju plus tak berhingga. |
| Fix | Membulatkan bilangan ke bilangan bulat terdekat menuju nol.. |
| Floor | Membulatkan bilangan ke bilangan bulat terdekat menuju minus tak berhingga. |
| Gcd | Menghitung nilai faktor pembagi terbesar |
| Isprime | Menghasilkan true jika merupakan bilangan prima. |
| Log10 | Menghitung logaritma suatu bilangan untuk dasar 10. |
| Mod | Menghitung nilai modulus. |
| Primes | Menghasilkan daftar bilangan. |
| Rem | Menghitung nilai remainder. |
| Round | Membulatkan bilangan ke bilangan bulat terdekat. |
2. Fungsi Trigonometri
Fungsi trigonometri banyak digunakan terkait dengan sudut. Nilai perhitungan yang dalam fungsi trigonometri sudut dalam radian.
Tabel 1.1b Fungsi Trigonometri
| Fungsi | Keterangan |
| Sin | Menghitung sinus suatu bilangan, dimana bilangan dalam radian. |
| Cos | Menghitung cosinus suatu bilangan, dimana bilangan dalam radian. |
| Tan | Menghitung tangen suatu bilangan, dimana bilangan dalam radian. |
| Acos | Menghitung arccosinus (invers cos) suatu bilangan yang menghasilkan sudut dalam radian, dimana bilangan harus antara -1 dan 1. |
| Asin | Menghitung arcsinus suatu bilangan yang menghasilkan sudut dalam radian, dimana bilangan harus antara -1 dan 1. |
| Atan | Menghitung arctangensuatu bilangan yang menghasilkan sudut dalam radian. |
| Cosh | Menghitung cosinus hiperbolik dari suatu sudut dalam radian. |
| Sinh | Menghitung sinus hiperbolik dari suatu sudut dalam radian. |
| Tanh | Menghitung tangen hiperbolik dari suatu sudut dalam radian. |
| Cosd | Menghitung cosinus suatu bilangan, dimana bilangan dalam derajat. |
| Sind | Menghitung sinus suatu bilangan, dimana bilangan dalam derajat. |
| Tand | Menghitung tangen suatu bilangan, dimana bilangan dalam derajat. |
| Sec | Menghitung suatu bilangan, dimana bilangan dalam radian. |
| Csc | Menghitung suatu bilangan, dimana bilangan dalam radian. |
| Cot | Menghitung suatu bilangan, dimana bilangan dalam radian. |
3. Fungsi Analisis Data
Matlab menyediakan sejumlah fungsi penting untuk digunakan dalam meng-analisis data, antara lain ditunjukkan pada Tabel 1.1c.
Tabel 1.1c Fungsi Analisis Data
| Fungsi | Keterangan |
| Max | Menghasilkan nilai terbesar dari suatu vektor atau matriks |
| Min | Menghasilkan nilai terbesar dari suatu vektor atau matriks |
| Mean | Menghasilkan nilai mean |
| Dll | ….. |
Vektor dan Matriks dalam Matlab
a. Vektor
Vektor baris :
>> v = [-2 sin(45) 4 6]
v =
-2.0000 0.8509 4.0000 6.0000
>> length(v) % menghitung panjang vektor
ans =
3
Vektor kolom :
>> x = [6; 5 ; 9]
x =
6
5
9
b. Matriks
Dapat diasumsikan bahwa didalam matlab setiap data akan disimpan dalam bentuk matriks. Dalam membuat suatu data matriks pada matlab, setiap isi data harus dimulai dari kurung siku ‘[‘ dan diakhiri dengan kurung siku tutup ‘]’. Untuk membuat variabel dengan data yang terdiri beberapa baris, gunakan tanda ‘titik koma’ (;) untuk memisahkan data tiap barisnya.
Matlab menyediakan beberapa fungsi yang dapat kita gunakan untuk menghasilkan bentuk-bentuk matriks yang diinginkan. Fungsi-fungsi tersebut antara lain:
- zeros : untuk membuat matriks yang semua datanya bernilai 0
- ones : matriks yang semua datanya bernilai 1
- rand : matriks dengan data random dengan menggunakan distribusi uniform
- randn : matris dengan data random dengan menggunakan distribusi normal
- eye : untuk menghasilkan matriks identitas
Cara Menginputkan Matrik.
Contoh :
Matrik A=
Ada 4 cara untuk menginputkan matrik yakni :
Cara 1:
>>a=[1 2 3;4 5 6;7 8 9]
Cara 2 :
>>a=[1 2 3 enter
- 5 6 enter
- 8 9];
Cara 3:
>>a1=[1 2 3];
>>a2=[4 5 6];
>>a3=[7 8 9];
>>a=[a1;a2;a3;];
>>a
Cara 4 :
>>a=input(‘Masukkan matrik= ‘);
>>Masukkan matrik=[1 2 3;4 5 6;7 8 9]
>>disp(a)
Operasi dan Fungsi pada Matriks
- Tabel 1.2. Operasi dan fungsi pada matriks yang sering digunakan :
| Perintah | Keterangan | Contoh |
| Det | Menghasilkan determinan matriks | Det(A) |
| Size | Menghasilkan ukura matriks | Size(A) |
| + | Menjumlahkan matriks | C = A + B |
| * | Mengalikan matriks | C = A * B |
| .* | Mengalikan elemen dengan elemen, dengan ketentuan memiliki ukuran yang sama | C = A .* B |
| ^ | Memangkatkan matriks dengan suatu skalar | C = A^ k |
| .^ | Memangkatkan elemen per elemen matriks dengan skalar | C = A .^ k |
| ’ | Transpose matriks | A’ |
| ./ | Membagi elemen per elemen dengan ketentuan memiliki ukuran yang sama | C = A ./ B |
| \ | Menghasilkan solusi AX = B | C = A \ B |
| / | Menghasilkan solusi XA = B | C = A / B |
| Inv | Menghasilkan invers matriks dengan ketentuan matriks merupakan matriks bujur sangkar | C = Inv(A) |
Grafik Matlab
Grafik 2 Dimensi
- Command Plot
>> Plot (X,Y,’ro’)
>> Plot (Nilai fungsi,fungsi,’warna_garis/data_point’)
- Colors : b(blue), r(red), g(green), y(yellow), m(magenta),
c(cyan), k(black)
- Markers : (o),(x),(*),(.),(+),(d),(s),(p),(h)
- Line Style : (-),(:),(-.),(- -),
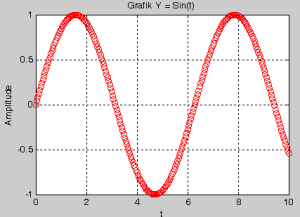
Contoh 1 :
>>n = 25
>>t = 0 : 1/n : 10
>>y = sin(t);
>>plot (t,y,’ro’)
>>title (‘Grafik Y = Sin(t)
>>grid
>>xlabel(‘t’), >>ylabel(‘Amplitude’)
Hasil Plot :
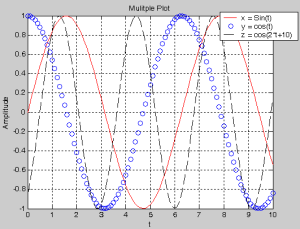
Contoh 2 : Menampilkan 2 grafik dalam 1 bidang
>>t=0:0.1:10;
>>x=sin(t);
>>y=cos(t);
>>z=cos(2*t+10);
>>plot(t,x,’r-‘)
>>hold on
>>plot(t,y,’bo’)
>>hold on
>>plot(t,z,’k–‘)
>>title(‘Mulitple Plot’)
>>xlabel(‘t’),ylabel(‘Amplitude’)
>>grid
>>legend(‘x=Sin(t)’,…
‘y=cos(t)’,’z=cos(2*t+10)’)
>>hold off
Hasil Plot :
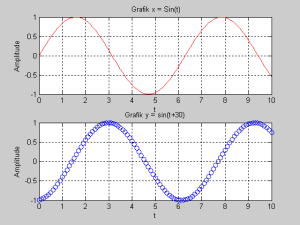
Contoh 3 : Menampilkan 2 grafik dalam 2 bidang (terpisah)
>> t=0:0.1:10;
>> x=sin(t);
>> y=sin(t+30);
>> subplot(2,1,1)
>> plot(t,x,’r-‘)
>> grid on
>>xlabel(‘t’),ylabel(‘Amplitude’)
>> title(‘ Grafik x = Sin(t)’)
>> subplot(2,1,2)
>> plot(t,y,’bo’)
>> grid on
>> xlabel(‘t’),ylabel(‘Amplitude’)
>> grid on
>> title(‘Grafik y = sin(t+30)’)
>> hold off
Hasil Plot :
Grafik 3 Dimensi
Matlab mempunyai heberapa fungsi tersendiri untuk memplot 3-D object. Fungsi-fungsi terscbut adalah plot kurva di ruangan (plot3). mesh surfaces (mesh), surfaces (surf) dan plot kontur (countour). Juga ada dua fungsi untuk memplot permukaan yang khusus, sphere dan cylinder.Untuk Iebih mengetahui 3-D graphic, ketikkan help graph3d Command Window.
Contoh :
>> n=25;
>> x=0:1/n:3;
>> plot3(x,sin(5*x),sin(5*x));
>> grid
Hasil Plot :
Matematika Dalam Teknik Kontrol
Fungsi Polinomial
Matlab menyediakan fungsi operasi standar dari polinom, seperti akar poli-nomial, evaluasi, dan turunan. Sebagai tambahan, fungsi-fungsi berikut diberikan untuk aplikasi lebih lanjut, seperti pencocokan kurva dan ekspansi fraksi parsial.
| Fungsi | Keterangan |
| Conv | Perkalian polinomial |
| Deconv | Pembagian polinomial |
| Poly | Polinomial dengan akar-akar tertentu |
| Polyder | Turunan polinomial |
| Polyfit | Pencocokan kurva polinomial |
| Polyval | Evaluasi polinomial |
| Polyvalm | Evaluasi matrik polinomial |
| Residue | Ekspansi fraksi parsial |
| Roots | Mencari akar-akar polinomial |
Transformasi
a). Transformasi Laplace
Contoh :
Tentukan transformasi laplace dari fungsi berikut ini :
f = 0,03(1-cos2t)
Jawab : Command windows :
>> f = sym(‘1-cos2*t)’)
>> F = laplace(f)
Atau pada M-file :
Syms t % Untuk inisialisasi variabel
f = 1-cos2*t
laplace(g)
b). Invers Laplace
Contoh :
Tentukan invers transformasi laplace dari fungsi berikut :
F(s) =
Jawab :
Command Windows :
>> F = exp(-1)/(s-1)
>> f = ilaplace(f)
Atau pada M-File :
Syms s % Untuk inisialisasi variabel
F = exp(-1)/(s-1)
ilaplace(F)
Differensial
Contoh :
- Turunan pertama dari fungsi y
>> syms x; ¿
>> y=x^3+2*x^2+6*x+7; ¿
>> z=diff(y) ¿
Akan muncul sebagai berikut :
z =
3*x^2+4*x+6
- Turunan kedua dari fungsi y
>>z=diff(y,2) ¿
Akan muncul sebagai berikut :
z =
6*x+4
Kontrol PID
PID Controller merupakan salah satu jenis pengatur yang banyak digunakan. Selain itu sistem ini mudah digabungkan dengan metoda pengaturan yang lain seperti Fuzzy dan Robust. Sehingga akan menjadi suatu sistem pengatur yang semakin baik Tulisan ini dibatasi pada sistem dengan Unity Feedback System, yang gambarnya sebagai berikut :
Gambar Block Diagram Untuk Unity Feedback System
- Tiga Jenis Controller dan karakteristiknya:
- Kontroler Proporsional (P)
Pengaruh pada sistem :
- Menambah atau mengurangi kestabilan
- Dapat memperbaiki respon transien khususnya : rise time, settling time.
- Mengurangi waktu naik, tidak menghilangkan Error steady state
Untuk menghilangkan Ess, dibutuhkan KP besar, yang akan membuat sistem lebih tidak stabil.
1. Kontroler Integral (I)
Pengaruh pada sistem :
- Menghilangkan Error Steady State
- Respon lebih lambat (dibanding P)
- Dapat menimbulkan ketidakstabilan (karena menambah orde sistem)
2. Kontroler Derivatif (D)
Pengaruh pada sistem :
- Memberikan efek redaman pada sistem yang berosilasi sehingga bisa memperbesar pemberian nilai Kp .
- Memperbaiki respon transien, karena memberikan aksi saat ada perubahan error.
- D hanya berubah saat ada perubahan error, sehingga saat ada error statis D tidak beraksi Sehingga D tidak boleh digunakan sendiri.
Fungsi transfer dari PID controller akan tampak sebagai berikut :
KP + + KDs =
- KP = Proportional Gain
- KI = Integral Gain
- KD = Derivatif Gain
Tabel Respon PID Controller Terhadap Perubahan Konstanta
| Respon Loop Tertutup | Waktu Naik | Overshoot | Waktu Turun | Kesalahan Keadaan Tunak |
| Kp | Menurun | Meningkat | Perubahan Kecil | Menurun |
| Ki | Menurun | Meningkat | Meningkat | Hilang |
| Kd | Perubahan Kecil | Menurun | Menurun | Perubahan Kecil |
Simulasi Sistem
Simulasi dengan M-File
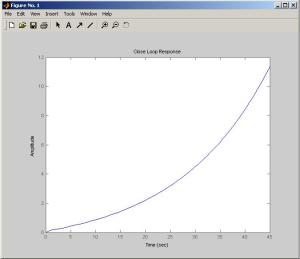
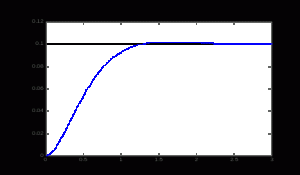
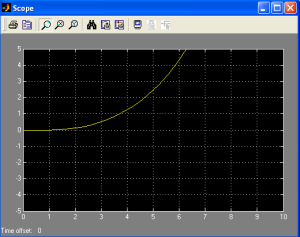
Untuk meng-analisa suatu sistem, software hanya memerlukan masukan berupa transfer function yang ditulis dalam Laplace Transform (dalam s-domain) atau matriks. contoh, suatu sistem kontrol memiliki transfer function sebagai berikut :
Ketikkan listing berikut pada M-File :
num = [1];
den = [1 2 10];
step(num,den)
title(‘Open Loop Response’)
Respon sistem terbuka (open loop response) dapat dilihat pada gambar di bawah ini :
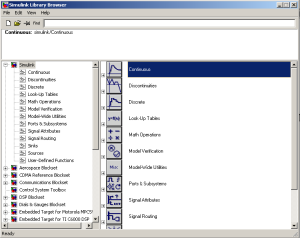
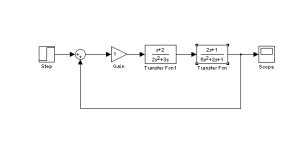
Simulasi dengan Simulink
Pada M-File kurva respon sistem dibuat dengan menggunakan listing program, sedangkan pada simulink kita bisa menganalisa sistem dengan menggunakan block diagram.
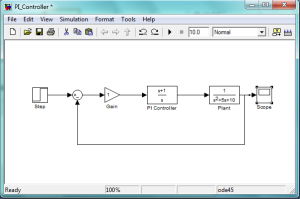
Analisa dengan mennggunakan simulink:
IV. TUGAS DAN JAWABAN
1. Buatlah matriks A dan B ordo 4×4, dan tentukan :
>> A=[ 6 5 8 7 ; 4 6 7 4 ; 3 4 2 8 ; 8 4 6 2 ]
A =
6 5 8 7
4 6 7 4
3 4 2 8
8 4 6 2
>> B=[ 5 4 6 7 ; 5 7 8 9 ; 8 6 4 2 ; 8 7 4 6 ]
B =
5 4 6 7
5 7 8 9
8 6 4 2
8 7 4 6
1. Invers matriks A dan B
>> inv(A)
ans =
-0.0525 -0.1377 0.0623 0.2098
-0.3902 0.3508 0.1508 0.0607
0.2820 -0.0098 -0.2098 -0.1279
0.1443 -0.1213 0.0787 -0.0770
>> inv(B)
ans =
0.2809 -0.2697 0.0618 0.0562
-0.4944 0.3146 0.0112 0.1011
0.1180 0.1067 0.2360 -0.3764
0.1236 -0.0787 -0.2528 0.2247
2. A x (B – 1)
>> A*(B-1)
ans =
149 130 110 119
117 107 95 99
98 91 73 92
104 90 92 96
3. Invers A x B
>> inv(A)*B
ans =
1.2262 0.6689 -0.3279 -0.2230
1.4951 2.2246 1.3115 1.0918
-1.3410 -1.0951 0.2623 0.6984
0.1279 -0.3393 -0.0984 -0.3869
4. A2
>> A^2
ans =
136 120 141 140
101 100 112 116
104 79 104 69
98 96 116 124
5. Elemen matriks A dan B dengan 4
>> A=[ 4 4 4 4 ; 4 4 4 4 ; 4 4 4 4 ; 4 4 4 4 ]
A =
4 4 4 4
4 4 4 4
4 4 4 4
4 4 4 4
>> B=[ 4 4 4 4 ; 4 4 4 4 ; 4 4 4 4 ; 4 4 4 4 ]
B =
4 4 4 4
4 4 4 4
4 4 4 4
4 4 4 4
6. Pangkatkan dengan 2 setiap matriks A dan B
>> A.^2
ans =
16 16 16 16
16 16 16 16
16 16 16 16
16 16 16 16
>> B.^2
ans =
16 16 16 16
16 16 16 16
16 16 16 16
16 16 16 16
7. Determinan matriks A dan B
>> det A
ans =
65
>> det B
ans =
66
2. Ubah persamaan liner berikut menjadi persamaan matriks dan cari nilai x1, x2, x3, dan x4 !
2×1 + x2 + 4×3 + 5×4 = 8
x1 – 2×2 – 1×3 + 5×4 = 4
9×1 + 3×2 + 3×3 + 4×4 = 10
4×1 + 3×2 + 7×3 – 1×4 = 47
Jawab :
>> A = [2 1 4 5 ; 1 -2 -1 5 ; 9 3 3 4 ; 4 3 7 -1]
A =
2 1 4 5
1 -2 -1 5
9 3 3 4
4 3 7 -1
>> B = [8;4;10;47]
B =
8
4
10
47
>> C = inv(A)*B
C =
5.9000
-17.3000
10.0000
-5.3000
>> x1=5.9000;x2=-17.3000;x3=10.0000;x4=-5.3000;
>> B=[x1;x2;x3;x4]
B =
5.9000
-17.3000
10.0000
-5.3000
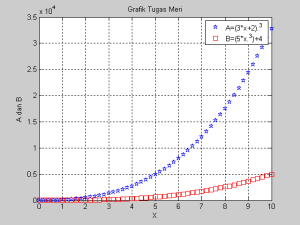
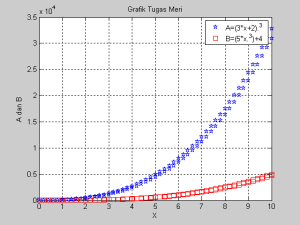
3. Buat tampilan grafik plot, stem, bar, dan stair dari 2 persamaan dalam 1 grafik! :
A = (3x+2)3 Dimana : n = 5;
B = 5x3+4 x = 0 : 1/n : 10
Jawab :
– Bahasa programnya
n=5
x=0: 1/n :10
A=(3*x+2).^3
B=(5*x.^3)+4
plot(x,A,’bp’)
hold on
plot(x,B,’rs’)
hold on
title(‘Grafik Tugas Meri’)
xlabel(‘X’),ylabel(‘A dan B’)
grid
legend(‘A=(3*x+2).^3′,’B=(5*x.^3)+4’)
hold off
Grafik Plot
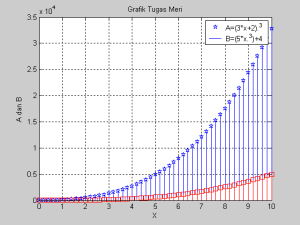
– Bahasa programnya
n=5
x=0: 1/n :10
A=(3*x+2).^3
B=(5*x.^3)+4
stem(x,A,’bp’)
hold on
stem(x,B,’rs’)
hold on
title(‘Grafik Tugas Meri’)
xlabel(‘X’),ylabel(‘A dan B’)
grid
legend(‘A=(3*x+2).^3′,’B=(5*x.^3)+4’)
hold off
Grafik Stem
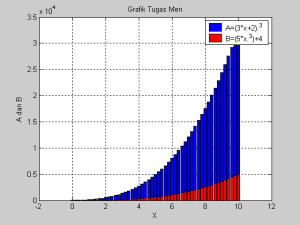
Bahasa Programnya:
n=5
x=0: 1/n :10
A=(3*x+2).^3
B=(5*x.^3)+4
bar(x,A,’bp’)
hold on
bar(x,B,’rs’)
hold on
title(‘Grafik Tugas Meri’)
xlabel(‘X’),ylabel(‘A dan B’)
grid
legend(‘A=(3*x+2).^3′,’B=(5*x.^3)+4’)
hold off
Grafik Bar
Bahasa Programnya:
n=5
x=0: 1/n :10
A=(3*x+2).^3
B=(5*x.^3)+4
stairs(x,A,’bp’)
hold on
stairs(x,B,’rs’)
hold on
title(‘Grafik Tugas Meri’)
xlabel(‘X’),ylabel(‘A dan B’)
grid
legend(‘A=(3*x+2).^3′,’B=(5*x.^3)+4’)
hold off
Grafik Stairs
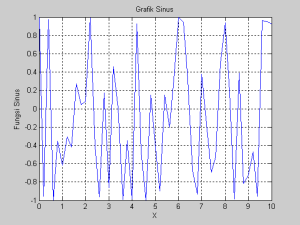
- Bagaimana cara menampilkan dua fungsi sinus dan cosinus pada masing fungsi yang disajikan dalam grafik yang berbeda. Misalnya anda gunakan contoh kasus pada soal ke-3, fungsi pertama anda tampilkan pada figure (1),sementara fungsi kedua anda tampilkan pada figure (2)!
Jawab:
– bahasa programnya
n=5
x=0 : 1/n :10
A=(3*x+2).^3
B=(5*x.^3)+4
C=sin(A)
D=cos(B)
figure(1)
plot(x,C,’b-‘)
hold on
title(‘Grafik Sinus’)
xlabel(‘X’),ylabel(‘Fungsi Sinus’)
grid
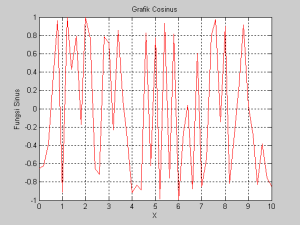
figure(2)
plot(x,D,’r-‘)
hold on
title(‘Grafik Cosinus’)
xlabel(‘X’),ylabel(‘Fungsi Sinus’)
grid
hold off
Grafik Soal No.3(Figure 1)
Grafik Soal No.3(Figure 2)
5. Tentukan transformasi fungsi laplace berikut:!
syms t
F= (t^3 + 3*t^2 + 4*t + 3)
laplace(F)
F =
t^3+3*t^2+4*t+3
ans =
6/s^4+6/s^3+4/s^2+3/s
- syms t
F= 3*(2*t-3)+(t-3)
laplace(F)
F =
7*t-12
ans =
7/s^2-12/s
- syms t
F= (3*sin(5*t*(pi/180)))
laplace(F)
F =
3*sin(1/36*t*pi)
ans =
1/12*pi/(s^2+1/1296*pi^2)
- syms t
F=(5*cos(3*t*(pi/180)))
laplace(F)
F =
5*cos(1/60*t*pi)
ans =
5*s/(s^2+1/3600*pi^2)
Tentukan transformasi Laplace balik dari fungsi-fungsi berikut:
- F(s) = ((s2 +3s +2)/(s3 +5s2 +10.5s +9))
Jawab :
syms s
F=((s^2 +3*s +2)/(s^3 +5*s^2 +10.5*s +9))
ilaplace(F)
F =
(s^2+3*s+2)/(s^3+5*s^2+21/2*s+9)
ans =
exp(-3/2*t)*cos(3/2*t)-1/3*exp(-3/2*t)*sin(3/2*t)
- F(s) = ((s+1)/(s3+6s2+11s+6))
Jawab :
syms s
F=((s+1)/(s^3+6*s^2+11*s+6))
ilaplace(F)
F =
(s+1)/(s^3+6*s^2+11*s+6)
ans =
-exp(-3*t)+exp(-2*t)
- F(s) = ((4s+5)/(s2+5s+18.5))
Jawab :
syms s
F=((4*s+5)/(s^2+5*s+18.5))
ilaplace(F)
F =
(4*s+5)/(s^2+5*s+37/2)
ans =
4*exp(-5/2*t)*cos(7/2*t)-10/7*exp(-5/2*t)*sin(7/2*t)
4. F(s) = ((s2-16)/(s3+8s2+24s+32))
Jawab :
syms s
F==((s^2-16)/(s^3+8*s^2+24*s+32))
ilaplace(F)
ans =
0
ans =
4*exp(-5/2*t)*cos(7/2*t)-10/7*exp(-5/2*t)*sin(7/2*t)
6. Buatlah gambar M-file dan simulink grafik keluaran sinyal dari TF persamaan berikut :
G(s) = s+2/2s2+3s
G(s) = 2s+1/5s2+2s+1
Jawab :
V. ANALISA
Pada praktikum kali ini, sebelum melakukan percobaan kami diperkenalkan dengan yang namanya Matlab, daerah lingkungan kerjanya, karakter-karakter spesial matlab yang juga perlu kita ketahui serta cara-cara meimplentasikan fungsi, vektor, matriks maupun grafik ke dalam matlab. Matlab adalah bahasa pemograman yang berbeda dengan bahasa pemograman tingkat tinggi seperti visual basic,Delphi dan lain-lain, matlab memiliki kelebihan sendiri yaitu dapat menyelesaikan persoalan komputasi teknis, visualisasi dan pemrograman seperti komputasi matematik, analisis data, pengembangan algoritma, simulasi dan pemodelan dan grafik-grafik perhitungan.
Matlab memiliki aturan/kaidah sendiri dalam penulisan perintah programnya misalnya kita ingin membuat persamaan matriks maka kita harus mengawalinya dengan tanda [ dan diakhiri tanda ] serta tanda ; sebagai pemisah baris satu dan baris selanjutnya. Dan untuk mengetahui invers atau determinan dari matriks tersebut kita tinggal berikan perintah inv atau det. Bukan hanya matriks, bisa juga turunan,integral,laplace, laplace balik dan lain-lain.
Selain dapat menyelesaikan perhitungan matematik,MatLab juga dapat menyajikan data input dalam tampilan Grafik. Grafik yang disajikan dapat berupa 3D atau 2D berupa plot, stem, bar atau stair. Tergantung bagaimana input yang kita berikan. Bahkan matlab juga dapat bermanfaat untuk pengoperasian fungsi laplace dan membuat diagram blok. PID controller yang merupakan salah satu jenis pengaturan yang dilakukan dapat disimulasikan dengan metode Simulink pada matlab. Setelah melakukan banyak percobaan diatas saya baru mengerti bahwa dalam penulisan perintah program pada matlab diperlukan ketelitian yang sangat tinggi karena salah sedikit saja maka pesan error akan ditampilkan , tapi disini matlab lagi-lagi memliki kelebihan ketika mengalami kesalahan atau error maka matlab akan memberitahu kita baris mana yang mengalami kesalahan penulisan program tersebut, sehingga kita tidak susah lagi untuk mencari kesalahan dimana yang terjadi.
VI. KESIMPULAN
- Software MATLAB mampu menyelesaikan persoalan komputasi teknis, visualisasi dan pemrograman seperti komputasi matematik, analisis data, pengembangan algoritma, simulasi dan pemodelan dan grafik-grafik perhitungan.
- MatLab memiliki sensitivitas yang tinggi dalam mengeksekusi input yang dimasukan.
- MATLAB mampu mensimulasikan suatu data masukan dengan tampilan 2 dimensi dan 3 dimensi.
- Fasilitas Simulink Windows pada MATLAB sangat membantu dalam simulasi kontrol (PID Controller).
- Software MATLAB, Matrix Laboratory, dikembangkan berdasarkan metode matrik (penggunaan baris dan kolom).
DAFTAR PUSTAKA
Korps Asisten Dasar Sistem Kendali. 2009. Modul Praktikum Dasar Sistem Kendali. Inderalaya : Universitas Sriwijaya
http://www.google.co.id/pengoprasian program matlab. Diakses tanggal 28 mei 2009.
http://www.members.ivcos.co.uk/roadevil/article.php?sid=2beton .Diakses tanggal 28 mei 2009.
http://www.rtcuifm@yexa.eng-ui.ac.id). Diakses tanggal 28 mei 2009.
http://www.blogspot.com/elektronika. Diakses tanggal 28 mei 2009.